Diamond-Square Algorithm

알고리즘 문제를 풀다가 Diamond-Square Algorithm 이라는 것을 발견하고, 문득 궁금해져서 포스팅을 하게 되었다.

이 알고리즘은 height-map을 생성하는 방법에 사용되며, 1982년 SIGGRAPH에서 Fournier, Fusseell 및 Carpenter에 의해 처음 소개되었다고 한다.

 

문제에 나온 설명은 아래와 같다.

"

이 알고리즘은 정사각형을 이루는 점 4개를 고르고 그 후에는 다음과 같은 과정을 거쳐 모양이 만들어진다.

정사각형의 각 변의 중앙에 점을 하나 추가한다.

정사각형의 중심에 점을 하나 추가한다.

그림1. 알고리즘 문제 그림

 

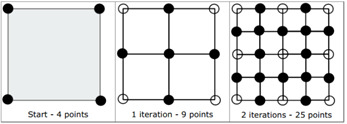
[그림]은 0단계(start)에서 2단계(2 iterations)까지 수행한 결과이다. 각 단계(N)가 계속해서 커져갈수록 점의 수가 커져간다.

"

 

 

이 알고리즘에 대한 설명이 많지 않아, 위키백과를 참고했다.

아래의 내용은 위키백과에 적힌 내용이다.

 

"

다이아몬드-스퀘어 알고리즘은 폭과 높이가 2n + 1 인 2차원 정사각형 배열로 시작한다. 

배열의 네 모서리 점은 먼저 초기 값으로 설정해야 한다.

그런 다음 모든 배열 값이 설정될 때까지 다이아몬드와 정사각형 단계가 번갈아 수행된다.

① 다이아몬드 단계 : 배열의 각 사각형에 대해 해당 사각형의 중간점을 네 모서리 점의 평균과 난수 값을 더한 값으로 설정한다.

② 정사각형 단계 : 배열의 각 다이아몬드에 대한 해당 다이아몬드의 중간점을 네 모서리 점의 평균과 난수 값을 더한 값으로 설정한다.

"

 

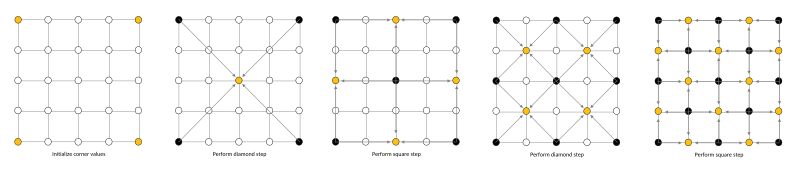
똑같은 내용을 조금 더 구체화적으로 표현해 설명해준 것 같다. 위키백과의 그림이 훨씬 더 이해가 수월했다.

 

해당 알고리즘을 활용한 문제를 풀기 위해서는 규칙을 찾아야 했다.

 

그림1을 보면, 시작 단계(0단계)에서는 정사각형 하나의 모서리 꼭짓점 4개로 표현된다.

1단계에서는 다이아몬드 단계-정사각형 단계를 한 번씩 거쳐서 점이 9개가 된다. (+5개)

2단계에서는 똑같은 과정을 거쳐서 점이 25개가 된다. (+16)

4 → 9 → 25 ...

2x2 → 3x3 → 5x5 ...

 

3단계를 해봐야 규칙을 찾을 수 있을 것 같았다.

3단계에서도 똑같은 과정을 거쳐서 점이 81개가 된다. (+56)

 

4 → 9 → 25 → 81

2x2 → 3x3 → 5x5 →9x9

이제서야 규칙이 보이기 시작했다.

 

점의 개수가 NxN으로 가정한다면,

2x2 → 3x3의 경우 N이 2^0만큼 증가했다. 

3x3 → 5x5의 경우 N이 2^1만큼 증가했다. 

5x5 → 9x9의 경우 N이 2^2만큼 증가했다. 

 

즉, N을 2로 설정하고 본다면

0단계에서는 NxN

1단계에서는 (N+2^0) x (N+2^0)

2단계에서는 (N+2^0+2^1) x (N+2^0+2^1)

3단계에서는 (N+2^0+2^1+2^2) x (N+2^0+2^1+2^2) 이런식으로 

n단계에서는 (N+ ... + 2^(n-1)) x (N+ ... + 2^(n-1))가 된다는 것이다.

 

이 알고리즘을 단순히 숫자로만 생각하고 문제를 푼다면 이 공식을 사용하면 풀린다.

 

 

 

⭐ 실제로 이 알고리즘은 풍경을 생성하는 데에 사용된다고 한다. 관심이 있다면 아래의 링크를 참고하면 좋을 것 같다.

 

https://janert.me/blog/2022/the-diamond-square-algorithm-for-terrain-generation/

The Diamond-Square Algorithm for Terrain Generation - Philipp K. Janert, Ph.D.

https://medium.com/@f.scaramelli0/heightmap-generation-using-the-diamond-square-algorithm-part-1-7c558aff7525

Heightmap generation using the Diamond Square algorithm — Part 1